
TASAPINNALISED KUJUNDID
RUUT
-
Ruut on võrdsete külgede ja nurkadega nelinurk
-
Ruudu kõik nurgad on täisnurgad
-
Ruudu diagonaalid on risti ja poolitavad teineteist
-
Ruudu diagonaal poolitab nurga
RUUDU ÜMBERMÕÕT
-
Ruudu ümbermõõt (P) võrdub külgede summaga
P=4a
RUUDU PINDALA
-
Ruudu pindala (S) võrdub külje a ruuduga
S=a²

RISTKÜLIK
-
Ristkülik on nelinurk, mille kõik nurgad on täisnurgad
-
Ristküliku vastasküljed on omavahel paralleelsed
-
Ristküliku diagonaalid poolitavad teineteist
RISTKÜLIKU ÜMBERMÕÕT
-
Ristküliku ümbermõõt (P) võrdub külgede summaga
P=2(a+b)
RISTKÜLIKU PINDALA
-
Ristküliku pindala (S) võrdub lähiskülgede korrutisega
S=ab



KOLMNURK
-
Lähisküljed on need kaks külge, mis moodustavad nurga
-
Kolmnurga tipus vastasküljele või selle pikendusele tõmmatud ristlõiku nimetatakse kolmnurga kõrguseks
-
Kolmnurga sisenurkade summa on 180°
KOLMNURGA ÜMBERMÕÕT
-
Kolmnurga ümbermõõt (P) võrdub külgede summaga
P=a+b+c
KOLMNURGA PINDALA
-
Kolmnurga pindala (S) võrdub aluse ja kõrguse poole korrutisega



KOLMNURKADE LIIGITAMINE
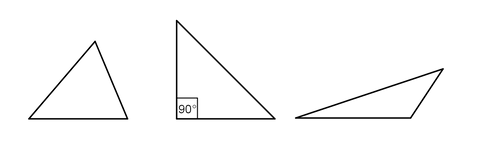
NURKADE JÄRGI
-
Teravnurkne kolmnurk
Kolm teravnurka, kõik väiksemad kui 90°
-
Täisnurkne kolmnurk
Üks täisnurk (90°) ja kaks teravnurka
-
Nürinurkne kolmnurk
Üks nürinurk (suurem kui 90°) ja kaks teravnurka
KÜLGEDE JÄRGI
-
Erikülgne kolmnurk
Kõik küljed on erineva pikkusega
Kõik nurgad on erineva suurusega
-
Võrdhaarne kolmnurk
Kaks külge ühepikkused ja üks külg erineva pikkusega
Alusnurgad on võrdsed
-
Võrdkülgne kolmnurk
Kõik kolm külge on ühepikkused
Kõik nurgad on 60°

TÄISNURKNE KOLMNURK
-
Täisnurka tähistatakse tavaliselt tähega C
-
Täisnurga lähiskülgesid nimetatakse kaatetiteks
-
Täisnurga vastaskülge nimetatakse hüpotenuusiks
-
Täisnurkse kolmnurga kaatetid on risti, järelikult pindala (S) võrdub kaatetite (ab) poole korrutisega
-
Pythagorase teoreem
a²+b²=c²
-
Eukleidese teoreem
a²=fc
b²=gc
-
Kõrguse teoreem
VÕRDHAARNE KOLMNURK
-
Kaks külge on ühepikkused, neid nimetatakse haaradeks
-
Üks külg on erineva pikkusega, seda nimetatakse aluseks
-
Aluse lähisnurgad on alusnurgad
-
Alusnurgad on võrdsed
-
Võrdhaarse kolmnurga tipunurga poolitaja poolitab ka aluse


a-kaatet
b-kaatet
c-hüpotenuus





RÖÖPKÜLIK
-
Rööpkülikuks nimetatakse nelinurka, mille vastasküljed on paralleelsed
-
Rööpküliku omadused:
Rööpküliku vastasküljed on võrdsed
Rööpküliku vastasnurgad on võrdsed
Rööpküliku nurki, mis asuvad ühe külje otspunktides nimetatakse lähisnurkadeks. Rööpküliku lähisnurkade summa on 180°
Rööpküliku diagonaalid poolitavad teineteist
-
Rööpküliku vastaskülgede või nende pikenduste vahelist ristlõiku nim. rööpküliku kõrguseks
-
Rööpkülikul on kaks erinevat kõrgust
-
Rööpküliku külge, millega kõrgus on risti nim. rööpküliku aluseks
-
Rööpkülikul on kaks alust ja kaks kõrgust
RÖÖPKÜLIKU ÜMBERMÕÕT
-
Rööpküliku ümbermõõdu leidmiseks tuleb tema lähiskülgede summa korrutada kahega
P=2(a+b)
RÖÖPKÜLIKU PINDALA
-
Rööpküliku pindala leidmiseks tuleb tema alus korrutada kõrgusega
S=ah
-
Ristkülik on rööpküliku erijuhtum, mille korral kõik nurgad on võrdsed
-
Ruut on ristküliku erijuhtum ja järelikult ka rööpküliku erijuhtum
VÕRDKÜLGNE KOLMNURK
-
Kõik küljed ühepikkused
-
Kõik nurgad ühesuurused




ROMB
-
Rombiks nimetatakse nelinurka, mille kõik küljed on võrdsed
-
Rombi omadused:
Romb on rööpküliku erijuhtum, tal on samad omadused mis rööpkülikulgi:
Rombi vastasküljed on paralleelsed
Rombi vastasnurgad on võrdsed
Rombi lähisnurkade summa on 180°
Erinevad omadused:
Rombi diagonaalid on risti ja poolitavad teineteist
-
Ruut on rombi erijuhtum
ROMBI ÜMBERMÕÕT
-
Rombi ümbermõõt võrdub neljakordse küljepikkusega
P=4a
ROMBI PINDALA
-
Rombi pindala võib arvutada nagu rööpküliku pindala: alus korda kõrgus
S=ah
-
Rombi pindala võrdub diagonaalide poole korrutisega


RING JA RINGJOON
-
Ringjoone kõik punktid asuvad ühel ja samal tasandil ja on ringjoone kekspunktist võrdsetel kaugustel
-
Ringi raadiuseks (r) nimetatakse ringi keskpunkti kaugust ringjoonest
-
Ringi diameetriks (d) nimetatakse sirglõiku, mis ühendab kaht ringjoone punkti ja läbib keskpunkti
-
Ringi diameeter on radiusest kaks korda pikem
d=2r
RINGJOONE PIKKUS
-
Iga ringjoone pikkus on selle diameetrist pii (π) korda suurem
-
Arvu pii väärtuseks võtame 3,14
-
Ringjoone pikkus (C) on võrdne arvu pii ja diameetri korrutisega
C=πd
C=2πr
RINGI PINDALA
-
Ringi pindala (S) võrdub arvu pii ja raadiuse ruudu korrutisega
S=πr²

TRAPETS
-
Trapetsiks nimetatakse nelinurka, mille kaks külge on paralleelsed ja kaks mitteparalleelsed
-
Trapetsi parallelseid külgi nimetatakse alusteks. Mitteparalleelseid nimetatakse haaradeks
-
Trapetsi aluste vahelist ristlõiku nimetatakse trapetsi kõrguseks
-
Trapetsi omadused:
Trapetsi haara lähisnurkade summa on 180°
Aluse lähisnurkasid nimetatakse alusnurkadeks. Võrdhaarse trapetsi alusnurgad on võrdsed
TRAPETSI ÜMBERMÕÕT
-
Trapetsi ümbermõõdu (P) leidmiseks tuleb leida kõik neli külge
P=a+b+c+d
TRAPETSI KESKLÕIK
-
Lõiku, mis ühendab trapetsi haarade keskpunkti nimetatakse trapetsi kesklõiguks (k)
-
Trapetsi kesklõik võrdub aluste poole summaga
TRAPETSI PINDALA
-
Trapetsi pindala (S) võrdub aluste pool summa ja kõrguse korrutisega
-
Trapetsi pindala võrdub kesklõigu ja kõrguse korrutisega
S=kh
VÕRDHAARNE TRAPETS
-
Trapetsit nimetatakse võrdhaarseks, kui tema haarad on võrdsed
TÄISNURKNE TRAPETS
-
Trapetsit nimetatakse täisnurkseks, kui tema haar on risti alusega


KORRAPÄRANE HULKNURK
-
Kõik küljed on ühepikkused
-
Sisenurgad ühesuurused
ÜMBERMÕÕT
PINDALA

c=e
-külg
n-külgede arv
m-apoteem
r-siseringjoone raadius
R-ümberringjoone raadius
m=r







RUUMILISED KUJUNDID
KOLNURKNE PÜSTPRISMA
-
Ruumikujund, mille tahud on kolmnurgad ja ristkülikud
-
Kolmnurksed tahud on põhjatahud ja nad on võrdsed
-
Ristkuküliku kujulised tahud on külgtahud
-
Prismal on tipud ja servad. Servad jagunevad põhjaservadeks ja külgservadeks. Külgservad on võrdsed ja langevad kokkku prisma kõrgusega (H)
PINDALA
-
Prisma täispindala (St) võrdub külgpindala (Sk) ja kahe põhja pindala (Sp) summaga
St=Sk+2Sp
-
Külgpindala (Sk) võrdub põhja ümbermõõdu (P=a+b+c) ja prisma kõrguse (H) korrutisega
Sk=PH
-
Prisma põhjaks on kolmnurk, seega põhjapindala (Sp) võrdub aluse ja kõrguse poole korrutisega
RUUMALA
-
Prisma ruumala (V) võrdub põhjapindala (Sp) ja kõrguse (H) korrutisega
V=SpH


PÜSTRÖÖPTAHUKAS
-
Keha, mille külgtahkudeks on ristkülikud ja põhjatahkudeks on rööpkülikud
-
Kaks põhjatahku (rööpkülikut)
-
Neli külgtahku (ristkülikut)
-
Kaheksa tippu
-
Kaksteist serva
Kaheksa põhjaserva
Neli külgserva, külgserva pikkust nimetatakse prisma kõrguseks (H)
PINDALA
-
Püströöptahuka täispindala (St) võrdub külgpindala (Sk) ja kahe põhja pindala (Sp) summaga
St=Sk+2Sp
-
Külgpindala (Sk) võrdub põhja ümbermõõdu [P=2(a+b)] ja prisma kõrguse (H) korrutisega
Sk=PH
-
Püströöptahuka põhjaks on rööpkülik, seega põhjapindala (Sp) võrdub aluse ja kõrguse korrutisega
Sp=ah
RUUMALA
-
Püströöptahuka ruumala (V) võrdub põhjapindala (Sp) ja kõrguse (H) korrutisega
V=SpH

KUUP
RUUMALA
V=a³
TÄISPINDALA
St=6a²
DIAGONAAL

AB-diagonaal

SILINDER
RUUMALA
V=πr²h
KÜLGPINDALA
Sk=2πrh
TÄISPINDALA
St=Sk+2Sp=2πrh+2πr²

ABCD-telglõige
RISTTAHUKAS
RUUMALA
V=abc
TÄISPINDALA
St=2(ab+ac+bc)
DIAGONAAL

AB-diagonaal

RUUMALA
KOONUS

KÜLGPINDALA
Sk=πrm
TÄISPINDALA
St=Sk+Sp=πrm+πr²
PÜSTPRISMA
RUUMALA
V=Sp·h
KÜLGPINDALA
Sk=Ph
TÄISPINDALA
St=Sk+2Sp
KERA
RUUMALA
PINDALA
S=4πr²


KORRAPÄRANE PÜRAMIID
m-külgtahu apoteem
RUUMALA
KÜLGPINDALA
TÄISPINDALA
St=Sk+Sp

